GUIA 3. RAZONAMIENTO GEOMÉTRICO.

GUIA. RAZONAMIENTO GEOMÉTRICO

PUNTO DE LLEGADA                                                                                                                                

                                   

ü  Usa herramientas para representar y explicar las conclusiones de los análisis realizados.

ü  Hace análisis de los datos recolectados para inferir ideas o conclusiones.

ACTIVIDADES DE PUNTO DE PARTIDA

·         ¿Qué crees que es razonamiento geométrico?

·         ¿Haz solucionado ejercicios de razonamiento geométrico antes?

·         ¿Para qué piensas que sirve estudiar el razonamiento geométrico?

COMPETENCIA PUNTO DE PARTIDA Y LLEGADA

Conoce los elementos y funcionalidades que tiene el uso de las fichas Nemotécnicas, para el desarrollo del Sistema Educacional Relacional Itagüí.

Piensa críticamente para opinar y decidir.

RECOLECCIÓN Y PROCESO DE INFORMACIÓN

1.        Realice lectura del tema razonamiento geométrico en el anexo consignado la final de la guía.

2.       Elabore una ficha nemotécnica de tipo resumen y comentario sobre el tema propuesto, que le permita más adelante diferenciar y solucionar  los diferentes tipos de problemas de razonamiento lógico trabajados en la cartilla.

DESARROLLO DE LA HABILIDAD

1.       Realice los ejercicios propuestos para el tema actual, el anexo mostrado al final de la guía.

RELACIÓN

1.      1.  Reúnete con otros compañeros e intercambia los procesos de pensamiento que tuvieron en cuenta para encontrar la respuesta a los ejercicios propuestos en la etapa de desarrollo de la habilidad. Hay diferencias?

2.       2. Completa la ficha nemotécnica elaborada en la etapa de recolección con las conclusiones que obtuviste al compartir información con tus compañeros y lo nuevo aprendido en la etapa de desarrollo de la habilidad. 

3.      3.  Describe qué elementos se facilitaron en el desarrollo del tema, cuáles se le dificultaron y qué cree que debe reforzar en el tema visto.

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 

ANEXO.

Razonamiento geométrico: se puede definir, como la unión entre la geometría (intuición y “visión”) con el razonamiento matemático.

El razonamiento geométrico se divide en cinco fases que dan cuenta del nivel de razonamiento geométrico que posee la persona; donde cada nivel está caracterizado por una forma distinta de comprensión y utilización de los conceptos geométricos, lo cual se refleja en una manera diferente de interpretarlos, definirlos, clasificarlos y hacer demostraciones.

El modelo de razonamiento geométrico más conocido, es el de Van Hiele, que fue desarrollado por los esposos, Dina y Pierre, Van Hiele, simultáneamente con la universidad de Utrecht (Rojas, C.), este modelo se encuentra dividido en dos etapas, la primera está dirigida exclusivamente a los estudiantes y permite realizar un acercamiento a los niveles de razonamiento geométrico en que se encuentran los estudiantes, esta primera etapa se encuentra dividida en cinco niveles y se denomina fases de razonamiento geométrico de Van Hiele.

El modelo de van hiele, permite que el docente haga una ³radiografía geométrica´ para determinar el nivel de razonamiento geométrico en que los estudiantes se encuentran y de esta manera aplicar estrategias que se encaminen a desarrollar habilidades en la resolución de problemas geométricos tanto aplicados como teóricos. Además, “los esposos van hiele plantean que el desarrollo de las habilidades de razonamiento geométrico, permite desarrollar habilidades de pensamiento y es facilitador del desarrollo intelectual de los estudiantes”. Por esta razón en la línea del modelo de los Van-Hiele, varios son los autores que, desde hace décadas, muestran la potencialidad del modelo para analizar el nivel de razonamiento en el trabajo geométrico, desarrollando a su vez nuevas estructuras o explicando las fases de una u otra manera.

A continuación, una  estructura de una prueba de razonamiento geométrico basada en el modelo Van Hiele, donde se muestra en cada nivel que se analiza.

Nivel 0 Visualización o razonamiento	Figuras y objetos
Nivel 1 Análisis	Partes y propiedades
Nivel 2 Ordenación o clasificación	Implicaciones entre propiedades
Nivel 3 Deducción formal	Deducción formal de teoremas

Según Fouz&Berritzegune, las fases de la primera etapa son denominadas de la siguiente manera:

Nivel 0: Visualización o reconocimiento. Según los autores, este nivel posee tres características que lo identifican, 1) los objetos se ven como un todo, es decir no hay una diferenciación entre los objetos que componen una determinada figura, no logran diferenciar los atributos que lo componen, 2) se hace una descripción del objeto asimilándolo a objetos familiares y comunes, no existe un lenguaje apropiado a la geometría para nombrar determinadas figuras y 3) no se reconocen de forma clara componentes y propiedades de los objetos con los que se trabaja.

Nivel 1: Análisis. En este nivel, los estudiantes identifican componentes y propiedades de los objetos y las figuras, sin embargo, aun no establecen relaciones entre propiedades o entre figuras y no poseen la capacidad para clasificar las propiedades y los objetos.

Nivel 2: Ordenación o clasificación. Este nivel posee tres características, 1) los estudiantes describen las figuras de manera formal, 2) se realizan clasificaciones lógicas de manera formal ya que el nivel de su razonamiento matemático ya esta iniciado y 3) siguen las demostraciones pero no las entienden en cuanto a su estructura, esto se da porque su nivel de razonamiento lógico es capaz de seguir pasos individuales de un razonamiento, pero no de asimilarlo en su totalidad. (Fouz&Berritzegune).

Nivel 3: Deducción formal. Se destacan algunos elementos por los cuales se puede identificar la llegada a este nivel, durante este nivel el estudiante logra hacer deducciones y demostraciones lógicas y formales, las relaciones se formalizan en conceptos axiomáticos, logran llegar a resultados similares o iguales partiendo de proposiciones distintas y lo que más caracteriza este nivel es que el estudiante logra crear una visión globalizadora de las matemáticas y se puede observar un alto nivel de razonamiento geométrico.

Nivel 4: Rigor. Se puede trabajar la geometría de manera abstracta sin necesidad de ejemplos concretos, alcanzándose el más alto nivel de rigor matemático. (Fouz&Berritzegune). Sin embargo, se considera que el estudiante que logre alcanzar un nivel3, posee suficiente capacidad de razonamiento geométrico, por lo tanto la mayoría de estudios realizados sobre el tema evalúan los niveles 1,2 y 3.

TALLER PROPUESTO

(NOTA: LOS PUNTOS 6,7,8,9 Y 13 NO SON OBLIGATORIOS PARA SEXTO)

1.     A partir del cuadrado formado con 12 palillos, como se muestra en la figura, retira dos palillos para obtener dos cuadrados. ¿Son del mismo tamaño los cuadrados obtenidos?

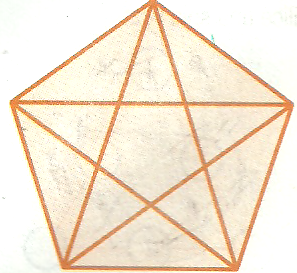
2.    ¿Cuántos triángulos diferentes puedes encontrar en la siguiente figura?

3.    El cuadrado de la figura de abajo está formado por 24 palillos y 9 cuadros iguales. Retira ocho palillos para obtener dos cuadrados, de manera que uno sea más pequeño que el otro. ¿Cuántas soluciones hay?

4.    Cuántos cuadrados de todos los tamaños posibles contiene la siguiente figura:

5.    A partir del siguiente cuadrado formado con 24 cerillas, quita 4 cerillas de manera que quede un cuadrado grande y cuatro cuadrados pequeños.

6.    Divide la pizza con tres líneas rectas de manera que  quede sólo un trozo de pimiento en cada porción.

7.    Intenta conectar cada rectángulo con el triángulo que tiene el mismo número. Las líneas no deben cruzarse ni salirse del diagrama.

8.    Fíjate si puedes unir cada cuadrado con el triángulo que tiene el mismo número. Las líneas no pueden cruzarse ni salirse del diagrama.

9.    Trata de unir los nueve puntos usando sólo cuatro líneas rectas. Nota: al trazar las líneas, no puedes alzar el lapicero.

10.  Intenta dividir, con dos líneas rectas, esta figura en tres partes que contengan la misma cantidad de bolitas.

11.  Agrega dos líneas rectas y divide el cuadrante del reloj en tres partes. La suma de los números de cada parte debe ser iguales.

12.  Fíjate si puedes hacer una tercera flecha que tenga el mismo tamaño que las otras dos agregando sólo dos líneas rectas.

13.  Dividir el pastel cilíndrico en 8 trozos iguales pero solamente con tres cortes.